डिजिटल इलेक्ट्रोनिकी
परिचय
[सम्पादन | स्रोत सम्पादित करें]इलेक्ट्रॉनिक परिपथ:-
इलेक्ट्रॉनिक परिपथ दो प्रकार के होते है
- एनालॉग परिपथ
- डिजिटल परिपथ
एनालॉग परिपथ
[सम्पादन | स्रोत सम्पादित करें]वे परिपथ जिनके वोल्टेज (अथवा धारा) में समय के साथ परिवर्तन होता रहता है एनालॉग परिपथ कहलाते हैं। इसमें वोल्टेज (अथवा धारा) को एनालॉग सिग्नल कहते हैं। जैसा कि आप (चित्र 1.0) में देख सकते हैं कि ग्राफ +4.80 से -4.80 तक के बीच में निरन्तर बदल रहा हैं। और यह ग्राफ सममित होता है अर्थात +4.80 से 0 तक और 0 से -4.80 तक ज्यावक्रीय (Sinusoidally) होता है।
डिजिटल परिपथ
[सम्पादन | स्रोत सम्पादित करें]
वे परिपथ जिनके वोल्टेज (अथवा धारा) में केवल दो स्तर होते हैं शुन्य या कोई एक स्थिर मान। डिजिटल परिपथ (Digital Circuit) कहलाते हैं। (चित्र 2.0) इसमें वोल्टेज (अथवा धारा) के स्तरो को डिजिटल सिग्नल (Digital Signal) कहते है।
- डिजिटल परिपथ के लिए बाइनरी संख्या प्रणाली का उपयोग किया जाता है जिसमें सिग्नल के दो स्तर केवल 0 और 1 से प्रदर्शित किये जाते हैं। इलेक्ट्रॉनिक कैल्कुलेटर भी एक डिजिटल युक्ति है क्योकि यह डिजिटल परिपथ 0 और 1 पर आधारित हैं। डिजिटल परिपथ का प्रयोग कम्प्युटर, रोबोट, इलेक्ट्रॉनिक तार-सचार, एसी, टीवी आदि में किया जाता हैं।
- डिजिटल परिपथ के फायदे
एनालॉग परिपथ के मुकाबले डिजिटल परिपथ आत्याधिक शक्तिशाली होते हैं। जिनके निम्न फायदे है:
- डिजिटल परिपथ सरल आकार, सुक्ष्म, हल्के, विश्वसनीय, सस्ते और स्थायी होते है।
- डिजिटल परिपथ प्रोग्रामिग (Programming) में प्रयोग किये जाते है।
- लॉजिक गेट्स का प्रयोग करके डिजिटल परिपथ को बडी आसानी से बनाया जा सकता है।
- डिजिटल परिपथो को एकीकॄत परिपथो (IC) में निर्मित किया जा सकता है।
लॉजिक गेट्स
[सम्पादन | स्रोत सम्पादित करें]लॉजिक गेट्स (Logic Gates) ऐसे डिजिटल परिपथ होते हैं जिसमें निवेशी (Input) और निर्गत (Output) सिग्नलो के बीच किसी तर्कसंगत सम्बन्ध को दर्शाया गया हो।
- लॉजिक गेट्स डिजिटल परिपथो के आधार स्तम्भ हैं। वे स्विचो, रिले, डायोडो, ट्रांजिस्टर और एकीकॄत परिपथो को प्रयुक्त करके बनाये जा सकते है।
लॉजिक गेट्स में एक अथवा एक से अधिक निवेशी (Input) टर्मिनल और एक निर्गत (Output) टर्मिनल होता हैं।
मूल लॉजिक गेट्स तीन है:
- OR गेट
- AND गेट
- NOT गेट
प्रत्येक मूल गेट का एक प्रतीक होता है जिसका प्रयोग सत्यता सारणी और बूलियन व्यंजक में किया जाता है
- सत्यता सारणी
किसी भी लॉजिक गेट में एक या एक से अधिक निवेशी टर्मिनल हो सकते हैं परंतु निर्गत टर्मिनल केवल एक होता हैं। निवेशी और निर्गत सिग्नलों के बीच सभी संभव मानो को एक सारणी में व्यक्त किया जाता हैं। इसे लॉजिक गेट की सत्यता सारणी कहते है।
- बूलियन व्यंजक
जॉर्ज बूल ने सन् 1854 में एक बीचगाणित का विकास किया जो तर्क कथनो पर आधारित थे। इसमें केवल दो अर्थ या मान हो सकते हैं सत्य अथवा असत्य।
OR गेट
[सम्पादन | स्रोत सम्पादित करें]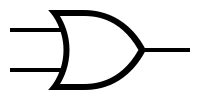
OR गेट की व्याख्या-एक या एक से अधिक टर्मिनल पर इनपुट देने से आउटपुट मिलता है
| इनपुट | आउटपुट | |
| A | B | Y = A OR B |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
डायोड सर्किट- इसमें दो या दो से अधिक डायोड P क्रम में लगाए जाते है और फारवड बायस दी जाती है
AND गेट
[सम्पादन | स्रोत सम्पादित करें]
| इनपुट | आउटपुट | |
| A | B | Y = A AND B |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
NOT गेट
[सम्पादन | स्रोत सम्पादित करें]
| इनपुट | आउटपुट |
| A | Y = NOT A |
| 0 | 1 |
| 1 | 0 |
NAND गेट
[सम्पादन | स्रोत सम्पादित करें]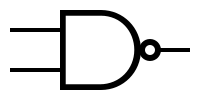
| इनपुट | आउटपुट | |
| A | B | A NAND B |
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
NOR गेट
[सम्पादन | स्रोत सम्पादित करें]
| इनपुट | आउटपुट | |
| A | B | A NOR B |
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 0 |
XOR गेट
[सम्पादन | स्रोत सम्पादित करें]
| इनपुट | आउटपुट | |
| A | B | A XOR B |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
XNOR गेट
[सम्पादन | स्रोत सम्पादित करें]
| इनपुट | आउटपुट | |
| A | B | A XNOR B |
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
